Perceptron

The foundational building block of neural networks is the perceptron - a binary classifier loosely modeled after a biological neuron.

Biological Neuron¶

Biological neurons typically look like this 👇

https://www.simplypsychology.org/neuron.html

This is one neuron. Not shown in this picture are the other ~86 billion neurons in your brain, connected to this one in an intricate web.

On the left side of this one neuron are its dendrites. Each dentrite is connected to another neuron.

On the right side of this neuron is the axon terminal. Other, downsteam neurons connect to this neuron via its axon terminal.

Information flows through the web of interconnected neurons in the form of electric or chemical signals.

The basic model goes like this:

1. This neuron receives information from other neurons via its dendrites.
2. This neuron processes the information and decides whether to emit a signal.
3. If the neuron emits a signal, the signal flows through the axon to the axon terminal, where this neuron's output signal becomes an input signal to downstream neurons.

Most neurons fire an all-or-nothing response. That is, they recieve a bunch of input signals, and they either output a signal (1) or they output nothing (0).

Perceptron Model¶

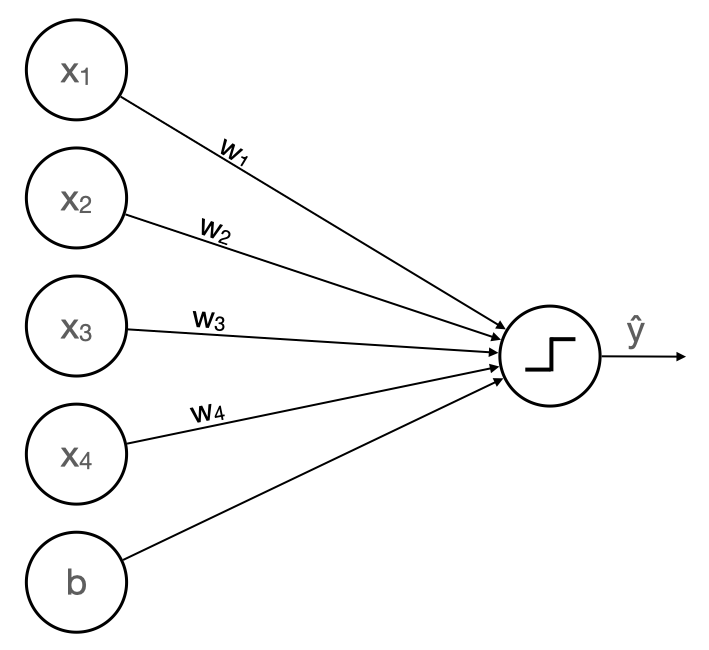
Inspired by biological neurons, the model of a perceptron is as follows

1. Start with an input vector: $\vec{x}$
2. Take a weighted sum of its components: $\vec{w}\cdot \vec{x}$
3. Add a bias (AKA offset) to the weighted sum: $\vec{w}\cdot \vec{x}+b$
4. If the sum is greater than or equal to 0, output 1, otherwise output 0

More formally,

Example¶

Suppose you want to build a model for 2x2 grayscale images to classify platforms.

A platform is just two dark cells on the bottom and two light cells on the top (kind of what an actual platform would look like from far away).

You collect the following training data.

    x1   x2   x3  x4  is_platform
0   10   67   63   9            0
1  252  221   68  32            1
2  212  253   39  60            1
3  196  231  214  60            0
4  115  174   51  15            0
5  134  253   15  25            0
6  180   65  238  33            0
7  242  206  183   3            0

is_platform is the target. x1, x2, x3, and x4 are the features.

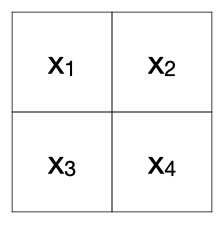
Four features means our perceptron model needs four weights.

Now suppose the 🧚 Perceptron Fairy visits our dreams to tell us the best weights and bias for the model are

Our updated perceptron model looks like this 👇

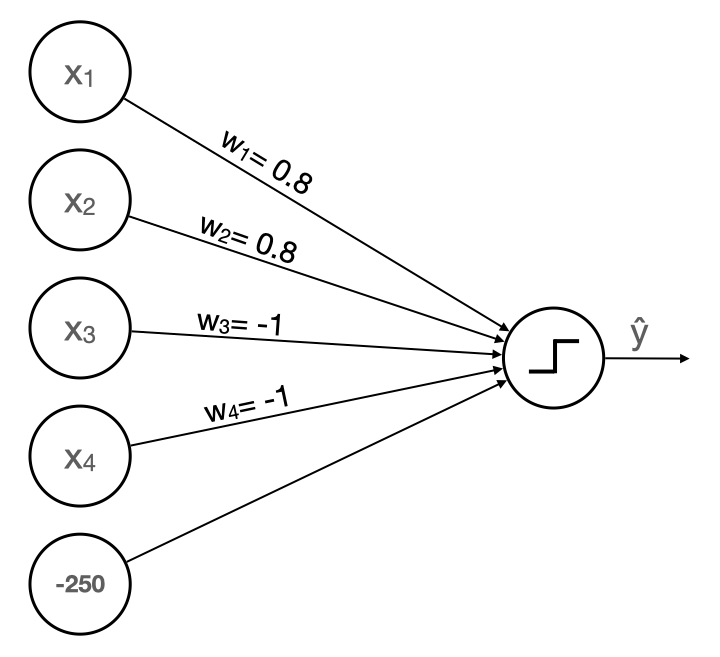
Calculating weighted sums plus bias and then thresholding gives us the following results

    x1   x2   x3  x4  is_platform      z  ŷ
0   10   67   63   9            0 -260.4  0
1  252  221   68  32            1   28.4  1
2  212  253   39  60            1   23.0  1
3  196  231  214  60            0 -182.4  0
4  115  174   51  15            0  -84.8  0
5  134  253   15  25            0   19.6  1
6  180   65  238  33            0 -325.0  0
7  242  206  183   3            0  -77.6  0

This model classifies the training data with 90% accuracy. Not perfect, but not bad .

So, why does it work?

Intuition¶

In our example, we can express the weighted sum as follows

Now think about pixel $x_1$. As its value increases (goes from dark to light), the weighted sum increases. In other words, lightening pixel $x_1$ adds evidence that the image is a platform. Similarly,

• lightening pixel $x_2$ increases evidence that the image is a platform
• lightening pixel $x_3$ decreases evidence that the image is a platform
• lightening pixel $x_4$ decreases evidence that the image is a platform

Furthermore, a certain amount of evidence is required to classify an image as a platform. How much evidence is implied by the bias (250).

Can you imagine a scenario where this behavior would be undesireable?

Drawback¶

Instead of classifying platforms, suppose we wanted to classify stairs.

In this case, should lightening pixel $x_1$ increase or decrease the evidence that the image depicts stairs?

It depends.

 ---- ----
| x1 | x2 |
|----|----|
| x3 | x4 |
 ---- ----

If $x_2$ is dark, then lightening $x_1$ should increase the evidence that the image depicts stairs. But if $x_2$ is light, then lightening $x_1$ should decrease the evidence that the image depicts stairs. Perceptrons can't handle this type of non-linear logic.

Choosing the weights and bias¶

Given some training data, how do we find the best weights and bias for a perceptron? There's a clever algorithm to do this called The Pocket Algorithm, but we won't cover it here. Soon we'll be using gradient descent, making The Pocket Algorithm somewhat obsolete.