Life's a garden. Dig it.
Challenge¶
Here's a "vanilla" 🍦 feed-forward neural network with logistic activation functions and softmax applied to the output layer.
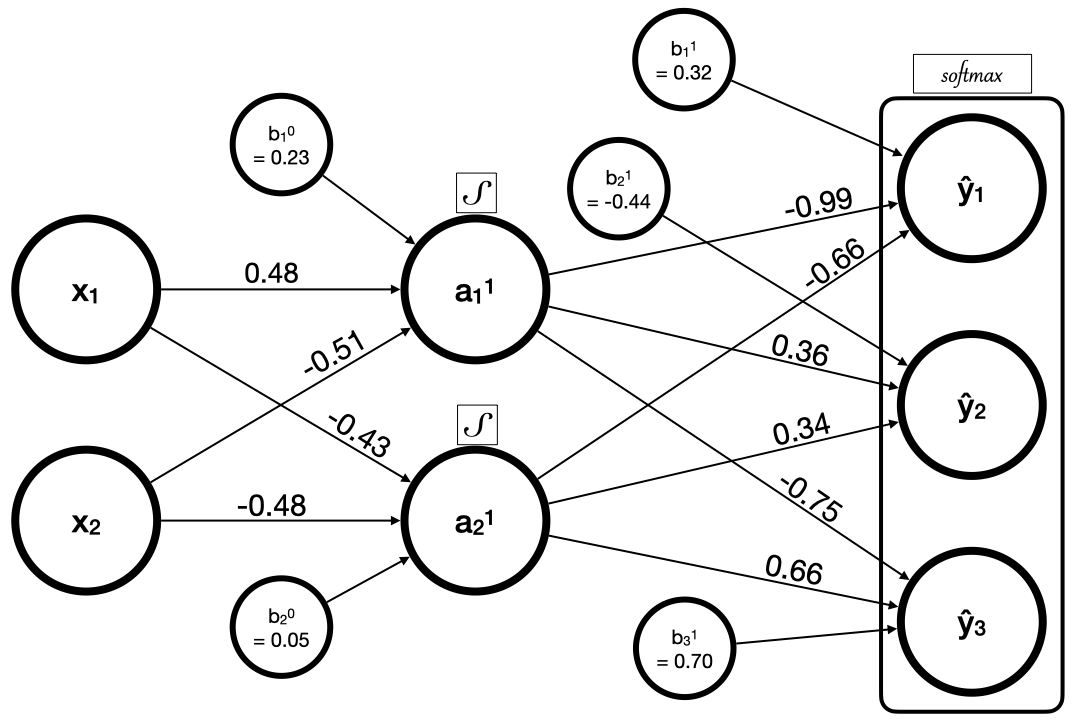
Given the following X and y tensors representing training data,
import torch
# Make data
torch.manual_seed(4321)
X = torch.rand(size=(8,2))
y = torch.randint(low=0, high=3, size=(8,))
print(X)
# tensor([[0.1255, 0.5377],
# [0.6564, 0.0365],
# [0.5837, 0.7018],
# [0.3068, 0.9500],
# [0.4321, 0.2946],
# [0.6015, 0.1762],
# [0.9945, 0.3177],
# [0.9886, 0.3911]])
print(y)
# tensor([0, 2, 2, 0, 2, 2, 0, 1])calculate:
- the predictions (forward pass)
- the loss using categorical cross entropy
- the gradient of the loss with respect to the weights and biases
Formulas¶
Logist Function
f ( x ) = 1 1 + e − x {\displaystyle f(x)={\frac {1}{1+e^{-x}}}} f(x)=1+e−x1
Softmax Function
σ ( z ) i = e z i ∑ j = 1 K e z j for i = 1 , … , K and z = ( z 1 , … , z K ) ∈ R K . {\displaystyle \sigma (\mathbf {z} )_{i}={\frac {e^{z_{i}}}{\sum _{j=1}^{K}e^{z_{j}}}}\ \ \ \ {\text{ for }}i=1,\dotsc ,K{\text{ and }}\mathbf {z} =(z_{1},\dotsc ,z_{K})\in \mathbb {R} ^{K}.} σ(z)i=∑j=1Kezjezi for i=1,…,K and z=(z1,…,zK)∈RK.
Categorical Cross Entropy Loss
J ( w ) = − 1 N ∑ n = 1 N [ y n log y ^ n + ( 1 − y n ) log ( 1 − y ^ n ) ] , {\displaystyle {\begin{aligned}J(\mathbf {w} )\ =\ -{\frac {1}{N}}\sum _{n=1}^{N}\ {\bigg [}y_{n}\log {\hat {y}}_{n}+(1-y_{n})\log(1-{\hat {y}}_{n}){\bigg ]}\,,\end{aligned}}} J(w) = −N1n=1∑N [ynlogy^n+(1−yn)log(1−y^n)],
Solution¶
This content is gated
Subscribe to the product below to gain access
