Life's a garden. Dig it.
Challenge¶
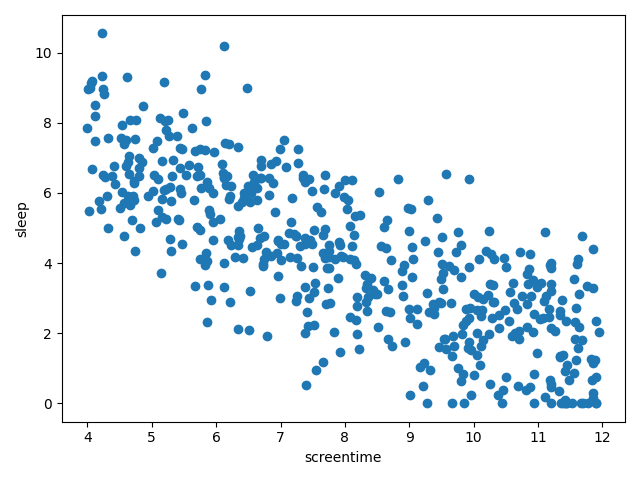
You suspect there's a linear relationship between how much daily screen time a person gets and how many hours they sleep. You acquire the data to investigate.
import numpy as np
rng = np.random.default_rng(123)
screentime = rng.uniform(low=4, high=12, size=500)
sleep = np.clip(-0.8*screentime + 10.5 + rng.normal(loc=0, scale=1.5, size=len(screentime)), 0, 24)
print(screentime[:5]) # [9.45881491 4.43056815 5.76287898 5.47497449 5.40724721]
print(sleep[:5]) # [2.87662678 6.24164643 6.14092628 4.54709214 5.24364 ]Plot
Fit a simple linear regression model to this data using gradient descent with the help of torch.autograd.
View the pseudocode
Solution¶
This content is gated
Subscribe to the product below to gain access
