Mar 05, 2025mathematics history problem-solving algorithms proof

The Sum of the Sum of Some Numbers

Mind-sized STEM ideas and experiments, beyond the textbook.

The-Sum-of-the-Sum-of-Some-Numbers

keywords: Gauss, von Neumann, Tartaglia, Abel, polynomials, combinatorics, mathematical proof, number theory

Carl Gauss' Very Bad Day¶

Johann Carl Friedrich Gauss has been called the Princeps mathematicorum (Latin for "the foremost of mathematicians" and anagram of "Anarchic Meets Impromptu"). He made many contributions to mathematics and science, and the British mathematician Henry John Stephen Smith said of Gauss,

If we except the great name of Newton it is probable that no mathematicians of any age or country have ever surpassed Gauss in the combination of an abundant fertility of invention with an absolute rigorousness in demonstration, which the ancient Greeks themselves might have envied.

Carl Friedrich Gauss

An apocryphal story of Gauss is that his teacher J.G. Büttner gave him detention for misbehaving in class, and told Gauss that he could go home when he'd added up all the numbers from $1$ to $100$ . Gauss immediately said $5050$ , and went home. Much later, Gauss' picture appeared on the German 10-Deutche Mark note.

Johnny von Neumann's Train Wreck¶

A similar story about mathematician John von Neumann is that he was at a party one time when someone asked him to solve a train problem.

John von Neumann

One train leaves New York heading toward Chicago and a second train leaves at the same time from Chicago for New York. (Stop me if you've heard this one before.) The distance between Chicago and New York is $800$ miles and both trains travel at $\; \text{mph}$ .

A very fast bee going $\text{ mph}$ takes off from the front of the NY to CHI train just as the train leaves the station (going $\text{ mph}$ ) and flies until it reaches the CHI to NY train. At that moment, it turns around and returns to the first train.

This continues until the trains meet in the middle, and due to a switching error, they're both on the same track and the bee gets squished in the wreckage. The problem was to figure out the total distance the bee flew on its final, fateful journey. You need to account for the positions of each train when the bee arrives and turns around.

avoid-train-wreck

John von Neumann instantly answered "600 miles".

"Oh, you must have known the trick" the other person said.

"What trick?" von Neumann asked, "I just summed up all of the individual distances."

There are an infinite number of distances between the trains as they approach each other, each distance smaller than the previous one. Von Neumann had to add them all together, and it's a bit like Zeno's "Achilles and the Tortoise" paradox.

The trick is that since both trains are going $\text{ mph}$ and the distance is $800$ miles, then when they crash into each other, they'll both have gone $400$ miles, taking $4$ hours. Since the bee flies at $\text{ mph}$ then its total distance would be $600$ miles.

I won't try to explain how von Neumann added up an infinite number of distances in his head so quickly, but we can understand how Gauss solved his detention problem. Think of the numbers arranged in a line, and connect the $1$ with $100$ , $2$ with $99$ , $3$ with $98$ , and so on.

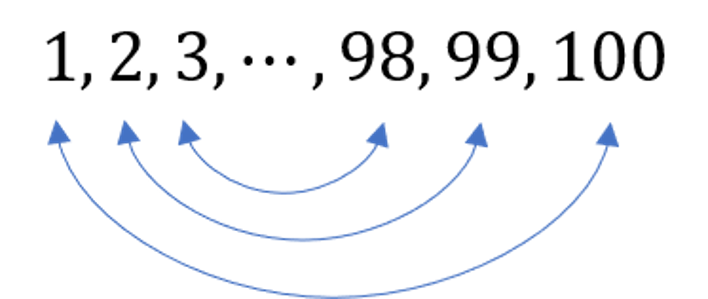
sum-of-100

Then the sum of $1 + 100 = 101$ , $2 + 99 = 101$ , $3 + 98 = 101$ , and the final pair is $50 + 51 = 101$ . Since there are $50$ pairs of $101$ then you can multiply $50 \times 100 = 5000$ and add $50$ to get the total $5050$ . You can check that the formula for the sum of the first $n$ numbers is $\frac{1}{2}n(n+1)$ .

Doubling Down on Gauss¶

A somewhat more complicated version of Gauss' detention problem is this. Suppose you have $n$ numbered tiles with numbers ranging from $\ldots, n$ . Add up all possible pairs and you'll get either the total sum $S_1 = 3,165,720$ or $S_2 = 3,165,620$ .

The question is, which is the correct total sum $S_1$ or $S_2$ , and what is the value of $n$ ? Daniel Hardisky proposed this problem for the Classical Mathematics Facebook group.

tiles

Let's start with an easy case, $n = 3$ . Then, we have to add the pairs together, $(1 + 2) + (2 + 3) + (3 + 1) = 12$ . Notice that each number appears twice, so we could have doubled $1 + 2 + 3 = 6$ .

Maybe it's just that easy. Let's try $n = 4$ . If we combine sequentially, we get $(1 + 2) + (2 + 3) + (3 + 4) + (4 + 1) = 20$ , but we've left out $(1 + 3)$ and $(2 + 4)$ which increases the final sum to $30$ .

How many ways can we combine two numbered tiles in a pile of $n$ tiles? This is a combinatorics problem and the answer is

\binom{n}{k} = \frac{n!}{(n-k)!k!}

where $\cdots 3 \cdot 2 \cdot 1$ . For the case of choosing $k = 2$ different tiles at a time, this simplifies to

\frac{1}{2}n(n-1).

Scientific computer languages have built-in functions to calculate the number of combinations for different values of $n$ and $k$ , in Julia, it's binomial(n,2), in R, use choose(n,k), and Python calls scipy.special.comb(n, k).

Octave also calculates the binomial expansion with nchoosek(n,k), but has a feature not found in other languages - you can replace $n$ with a vector to show all of the possible combinations of $n$ numbers taken $k$ at a time. The notation 1:5 is a vector containing the first $5$ integers, so we can have Octave return all of the combinations taken $2$ at a time,

>> nchoosek(1:5,2)
ans =
 
   1   2
   1   3
   1   4
   1   5
   2   3
   2   4
   2   5
   3   4
   3   5
   4   5

Even better, if we add the numbers in each row, we get every possible pair sum, and then adding those sums gives the total.

>> sum(sum(nchoosek(1:5,2)))
ans = 60

Maybe we can arrange the numbers to be similar to the way Gauss did his sum. If we add up all possible pairs for $n = 5$ , we can arrange them in descending order like this:

\begin{aligned} S = (5+4) + (5+3) + (5+2) &+ (5+1) \\ + (4+3) + (4+2) &+ (4+1) \\ + (3+2) &+ (3+1) \\ &+ (2+1). \end{aligned}

Notice the first line has four $5$ s and the sum $1 + 2 + 3 + 4$ . So, the top line is $\times 5 + (1+2+3+4) = 20 + 10 = 30$ . It's an easy multiplication followed by a sum using Gauss' trick. The next line is the same, but shorter, $\times 3 + (1+2+3) = 12 + 6 = 18$ .

For $n$ numbers the sum becomes

\begin{aligned} S = (n+(n-1)) + (n+(n-2))+ \cdots +(n+2) &+ (n+1) \\ + ((n-1)+(n-2)) + ((n-1)+(n-3))+ \cdots + ((n-1) + 2) &+ ((n-1)+1) \\ \vdots \\ + (5+4) + (5+3) + (5+2) &+ (5+1) \\ + (4+3) + (4+2) &+ (4+1) \\ + (3+2) &+ (3+1) \\ &+ (2+1). \\ \end{aligned}

If we collect all of the individual $n$ terms in the top two lines there are $n - 1$ of them, and then what's left is the sum of $\cdots + (n-1)$ , which can be written as

\sum_{j=1}^{n-1}j = n(n-1) + \frac{1}{2}(n-1)n.

The total sum for all of the terms is

\begin{aligned} S = S(n) = \left( n \cdot (n-1) + \sum_{j=1}^{n-1}j \right) + \left( (n-1) \cdot (n-2) + \sum_{j=1}^{n-2}j \right) + \cdots \\ + \left( 4 \cdot 3 + \sum_{j=1}^{4-1}j \right) + \left( 3 \cdot 2 + \sum_{j=1}^{3-1}j \right) + \left( 2 \cdot 1 + \sum_{j=1}^{2-1}j \right). \end{aligned}

Now we can sum up all of the individual terms,

\sum_{k=1}^{n-1}\left(k(k+1) + \sum_{j=1}^k j \right).

Since $\sum_{j=1}^k j = \frac{1}{2} k(k+1)$ , this can be expressed as

\begin{aligned} S(n) &= \sum_{k=1}^{n-1}\left(k(k+1) + \frac{1}{2}k(k+1)\right) \\ &= \frac{3}{2}\sum_{k=1}^{n-1} k(k+1) \\ &= \frac{3}{2}\sum_{k=1}^{n-1} k^2 + \frac{3}{2}\sum_{k=1}^{n-1} k \\ &= \frac{3}{2}\sum_{k=1}^{n-1} k^2 + \frac{3}{2} \left( \frac{1}{2} (n-1)n \right). \end{aligned}

Squared Pictures¶

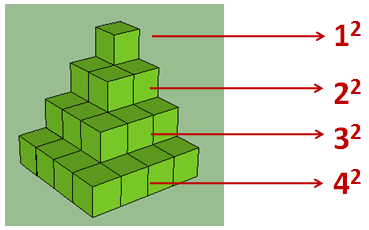
This is a pretty compact formula for $S (n)$ , the sum of all possible pairs of the numbers from $1$ to $n$ . But, can we find a better way to express $\sum_{k=1}^{n-1}k^2$ ? The first five squares are $1, 4, 9, 16, 25$ , and the sums are $1, 5, 14, 30, 55$ .

Here's a neat visual proof from the Math and Multimedia website. Make a stack of the first $n$ squares like this:

sum-of-squares1

Next, make three copies of this stack,

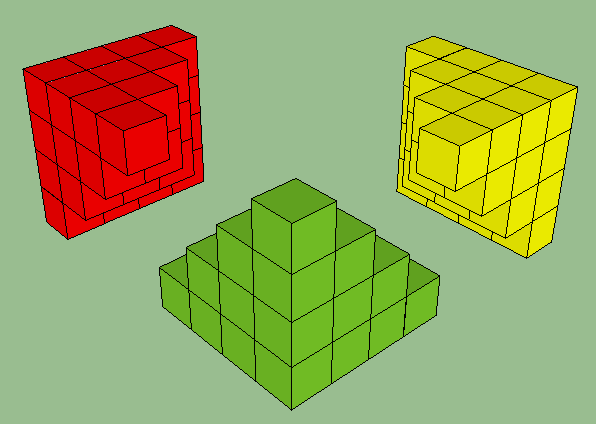
sumofsquares2

and fit them together to make a cube, except the red stack will extend one layer above the green and yellow stacks.

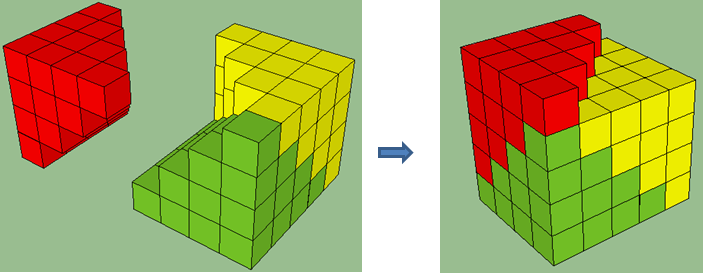
sum-of-squares-4

If you slice the top layer of the red pyramid in half and flip it over, you can fill in the missing part:

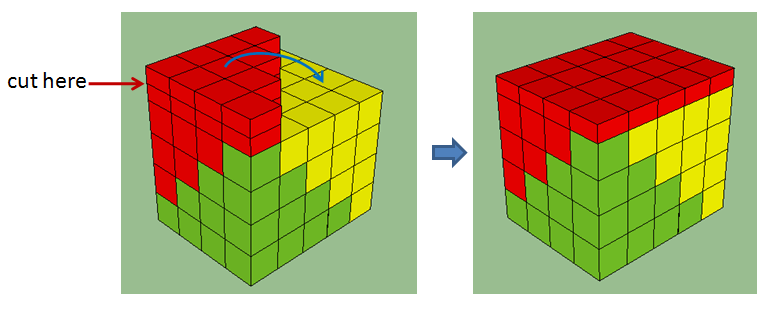
sum-of-squares-5

which lets us calculate the total volume,

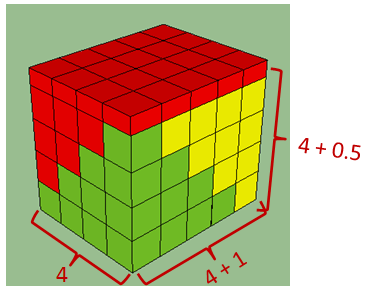
sum-of-squares-6

so we might expect the formula is

\begin{aligned} \sum_{k=1}^n k^2 &= \frac{1}{3}n(n+1)(n+\frac{1}{2}) \\ &= \frac{1}{6}n(n+1)(2n+1). \end{aligned}

The Proof¶

Pictures are helpful, but they aren't considered mathematical proofs. There are many ways to construct a mathematical proof, but one that gets used frequently is called "Proof by Induction".

Suppose you have a formula you think is correct, and you check it for the case $n = 1$ . If that holds, then show it holds for any $n - 1$ , and add the $n^{th}$ term to see if the formula still holds. Let's make this a bit more formal.

Theorem: The sum of the first $n$ squares is

\sum_{k=1}^{n} k^2 = \frac{1}{6}n(n+1)(2n+1).

Proof: For $n = 1$ ,

1^2 = 1 = \frac{1}{6}(1)(1+2)(2\cdot1+1) = \frac{1}{6}(1)(2)(3) = 1.

Assume the formula holds for the case $n - 1$ ,

\begin{aligned} \sum_{k=1}^{n-1} k^2 &= \frac{1}{6}(n-1)(n)(2(n-1)+1) \\ &= \frac{1}{6}n(n-1)(2n-1). \end{aligned}

Then the sum of the first $n$ squares is

\begin{aligned} \sum_{k=1}^{n-1}k^2 + n^2 &= \frac{1}{6}n(n - 1)(2n-1) + n^2 \\ &= \frac{1}{6} n (2n^2 -3n + 1) + n^2 \\ &= \frac{1}{6} (2n^3 -3n^2 + n) + \frac{1}{6}(6n^2) \\ &= \frac{1}{6} (2n^3 +3n^2 + n) \\ &= \frac{1}{6} n(2n^2 + 3n + 1) \\ &= \frac{1}{6} n(n+1)(2n + 1). \; \blacksquare \\ \end{aligned}

The inductive part of this proof is that we didn't specify a value for $n$ , so it can be any integer.

We showed the formula holds for $n = 1$ in the first part, so it must hold for $n = 2$ by the second part. Since it holds for $n = 2$ , then it must also be true for $n = 3$ and so on.

The Formula Simplified¶

And now, we have a complete formula for the sum of all possible pairs of the first $n$ numbers,

\begin{aligned} S(n) &= \frac{3}{2} \left( \frac{1}{6} n(n-1)(2n-1) + \frac{1}{2}n(n-1) \right) \\ &= \frac{3}{2} \left( \frac{1}{6} (n^2-n)(2n-1) + \frac{1}{2}(n^2-n) \right) \\ &= \frac{3}{2} \left( \frac{1}{6} (2n^3 -3n^2+n) + \frac{1}{6}(3n^2-3n) \right) \\ &= \frac{3}{2} \left( \frac{1}{6} (2n^3 - 2n) \right) \\ &= \frac{1}{2} (n^3 - n). \\ \end{aligned}

Tartaglia's Depression¶

Niccolò Fontana Tartaglia was a $16^{th}$ -century mathematician and engineer from Venice.

Nicolo Tartaglia

Tartaglia found a neat trick to convert a general cubic equation, $ax^3 + bx^2 + cx + d$ into a simpler form where the $x^2$ term disappears. By substituting $\frac{b}{3a}$ , he got the "depressed cubic" $y^3 + Ay = B$ .

With a bit of rearrangement, we can get our sum into the depressed cubic form,

n^3 - n = 2S,

where $A = - 1$ and $B = 2 S$ . In this form, the solution for $n$ is $n = s - t$ where

\begin{aligned} 3st &= A \\ s^3 - t^3 &= B. \end{aligned}

You can check this with a simple substitution. If we put $-\frac{1}{3s}$ from the first equation into the second, we get

\begin{aligned} s^3+\frac{1}{27s^3} = 2S \\ s^6 - 2Ss^3 + \frac{1}{27} = 0. \end{aligned}

Substituting $u=s^3$ gives the quadratic

u^2 - 2Su + \frac{1}{27} = 0

with solutions

\begin{aligned} u &= \frac{1}{2}\left(2S \pm \sqrt{4S^2 + \frac{4}{27}}\right) \\ &= S \pm \sqrt{S^2 + \frac{1}{27}}. \end{aligned}

Then, $\sqrt[3]{u}$ and $\frac{1}{3s}$ . Solving for $S_1 = 3165720$ gives $n_1 = 185$ , while $S_2 = 3165620$ gives $n_2 = 184.99805$ , so the first sum is the correct solution.

The Octave function depressedCubic.m calculates the solution for any depressed cubic in the form $x^3 + Ax = B$ .

Abel and the Terrible, Horrible, No Good, Very Bad Day¶

Niels Henrik Abel was a Norwegian mathematician who made many contributions to mathematics, and said of Gauss "He is like the fox, who effaces his tracks in the sand with his tail."

The Abel Prize, named in his honor is the mathematical equivalent of the Nobel Prize, and his picture appears on the Norwegian 500 kroner banknote.

Niels Henrik Abel

One of Abel's great contributions to mathematics was his proof that there is no closed-form solution to the quintic equation,

ax^5 + bx^4 + cx^3 + dx + e = 0,

which had been an open problem for 250 years. All in all, it was a great day for Abel, but a lousy day for anyone hoping to solve the equation directly, and we now know that no formula exists for the solution to fifth-order and higher polynomials.

Luckily, our problem involves only the quadratic formula and the solution to the depressed cubic.

The Schoolboy and the Fox: How Gauss Led Us to Modern Sum Theory¶

What started as a simple detention problem for young Gauss led us through a fascinating journey of mathematical discovery. We've seen how seemingly complex problems can often be simplified through clever visualization (like Gauss' pairing method), systematic analysis (as with our pair-sum formula), and historical mathematical innovations (like Tartaglia's depressed cubic).

The solution to our original question - finding which sum ( $S_1=3,165,720$ or $S_2 = 3,165,620$ ) is correct for the sum of all possible pairs of numbers from $1$ to $n$ - turned out to be $S_1$ with $n = 185$ . More importantly, we discovered how to solve this type of problem generally through the formula $\frac{1}{2}(n^3 - n).$

For the mathematically adventurous, this exploration opens doors to more complex combinations, though as Abel proved, we'll need to be careful about expecting neat solutions for higher-order polynomials. After all, mathematics, like the fox Gauss was compared to, often leaves fascinating trails for us to follow - even if some lead to mathematical dead ends.

If you're feeling adventurous, you could try finding a formula for the sum of all possible combinations of the first $n$ integers taken three at a time, four at a time, and so on. Of course, if you take them $n$ at a time, you're back to the beginning and the sum is $\frac{1}{2}n(n+1)$ .

Image credits¶

Hero: 10 DM Serie4 Vorderseite, Wikipedia.
Carl Friedrich Gauss: Carl Friedrich Gauss 1840 by Jensen, Wikimedia Commons.
John von Neumann: Von Neumann’s computer. George Dyson, Physics World, Dec. 06, 2012.
Nicolo Tartaglia: Niccolò Tartaglia Quesiti et inventioni diverse, Wikimedia Commons.
Niels Henrik Abel: Niels Henrik Abel, Academic Dictionaries and Encyclopedias.

Code and Software¶

depressedCubic.m - Solves the depressed cubic equation x^3 + Ax + B = 0 in Octave.

Julia - The Julia Project as a whole is about bringing usable, scalable technical computing to a greater audience: allowing scientists and researchers to use computation more rapidly and effectively; letting businesses do harder and more interesting analyses more easily and cheaply.
Octave - GNU Octave is a high-level language, primarily intended for numerical computations. It provides a convenient command line interface for solving linear and nonlinear problems numerically, and for performing other numerical experiments using a language that is mostly compatible with Matlab.
Python - Python is an interpreted, high-level and general-purpose programming language.

References and further reading¶

Zeno’s Paradoxes – Wikipedia.
- Discusses Zeno’s paradoxes, including Achilles and the Tortoise, which relate to the infinite sums discussed in the article.
Von Neumann’s Computer – George Dyson, Physics World, 06 Dec 2012.
- Provides historical context on John von Neumann’s contributions to mathematics and computing.
Combinations and the Binomial Theorem – Cuemath.
- Explains how to calculate combinations and their relevance to combinatorics.
The Abel Prize – Wikipedia.
- Provides an overview of the Abel Prize, named after Niels Henrik Abel, who made significant contributions to mathematics.
Sum of Squares Formula Proof – Math and Multimedia.
- A visual proof of the sum of squares formula, which is key to understanding the sum of pairwise sums.
Niccolò Tartaglia’s Mathematical Contributions – Wikimedia Commons.
- Covers Tartaglia’s work on cubic equations and their historical impact.
Niels Henrik Abel’s Life and Work – Academic Dictionaries and Encyclopedias.
- Provides biographical details on Abel and his proof that quintic equations have no general solution.
Carl Friedrich Gauss Biography – Wikimedia Commons.
- Covers Gauss' contributions to mathematics, including his famous summation trick.
The Depressed Cubic Equation – GitHub.
- A script that solves the depressed cubic equation, as discussed in the article.
Julia Programming Language – The Julia Project.
- Describes Julia, a programming language used for scientific computing.
GNU Octave – GNU Project.
- Documentation on Octave, a scientific computing environment used for numerical computations.
Anaconda Python Distribution – Anaconda.
- Explains the Python programming distribution used for numerical and scientific computing.
Facebook: Classical Mathematics Group – Facebook.
- A mathematics discussion group where the tile-sum problem was proposed.

📬 Subscribe and stay in the loop. · Email · GitHub · Forum · Facebook

The binomial coefficient $\binom{n}{k}$ , also called "n choose k," represents the number of ways to choose $k$ elements from a set of $n$ elements, without considering order. It is computed using the formula:

(nk)=n!k!(n−k)!\binom{n}{k} = \frac{n!}{k!(n-k)!}

This concept is widely used in combinatorics and probability theory.

Proof by induction is a mathematical technique used to prove statements for all natural numbers. It has two steps:

Base case: Verify the statement for the smallest value (e.g., $n = 1$ ).
Inductive step: Assume it is true for $n = k$ and prove it for $n = k + 1$ .

If both steps hold, the statement is true for all $n$ .

A quintic equation is a polynomial equation of degree five:

ax^5 + bx^4 + cx^3 + dx^2 + ex + f = 0

Niels Henrik Abel proved that no general formula exists for solving quintic equations using radicals, unlike quadratics, cubics, and quartics.