Mar 08, 2025chaos-theory mathematics programming julia interactive-learning

Easy Chaos with Pluto

Mind-sized STEM ideas and experiments, beyond the textbook.

Easy-Chaos-with-Pluto

keywords: chaos theory, Pluto notebook, logistic function, autocorrelation, phase portrait

Understanding the Predictably Unpredictable¶

Have you ever wondered why weather forecasts become unreliable beyond a few days? Or why your heart beats with slight irregularities even when you're perfectly healthy? These phenomena share a fascinating common thread: chaos theory, a branch of mathematics that explains how tiny changes can lead to dramatically different outcomes.

Chaos theory isn't just an academic curiosity - it's everywhere around us. From the turbulent flow of water from your faucet to the fluctuations in financial markets, from the patterns of animal populations to the spread of epidemics, chaos theory helps us understand complex systems that at first glance appear random but actually follow hidden patterns.

In this interactive tutorial, we'll use the power of Pluto notebooks and Julia programming to explore chaos theory hands-on. You'll discover how simple mathematical rules can generate surprisingly complex behavior, and learn why some systems are fundamentally unpredictable despite being completely deterministic.

Learning Objectives¶

By the end of this tutorial, you will be able to:

Set up and use Pluto notebooks for interactive mathematical exploration
Understand how linear systems behave differently from chaotic ones
Visualize and analyze the behavior of the logistic function
Interpret phase portraits and autocorrelation plots
Recognize sensitive dependence on initial conditions, a key feature of chaos
Apply these concepts to understand real-world chaotic systems

No advanced mathematics or programming experience is required - just bring your curiosity about how complexity emerges from simplicity. Let's dive in and make sense of chaos!

Getting Started with Pluto¶

Pluto is a notebook environment for Julia. Install Julia and start it to get a command window. The first step is to add some packages we'll use for this project. Type "]" at the prompt (without the quotes) to enter the package manager. The packages you'll need are:

add Pluto
add PlutoUI
add Plots
add StatsBase

It may take a few minutes as Julia checks and downloads all necessary dependencies. When everything has finished, type "Ctrl-C" to exit the package manager. In the Julia command window, type "Using Pluto" followed by "Pluto.run()":

julia-start-pluto

A new tab will open in your browser:

welcome-to-pluto

Download EasyChaos.jl from Github and then enter the path in Pluto below "Open from file:". The notebook should look very much like the remainder of this post.

Easy Chaos!¶

Pluto is a programming environment for Julia, designed to be interactive and helpful. Changes made anywhere in the notebook affect the entire notebook. Pluto is reactive so you don't need to recalculate cells.

This is useful in studying chaos because small changes made to a function can have big effects. You can define a function, run it, and immediately see the effects.

A Linear Equation¶

The equation of a line is $y = m x + b$ where $m$ is the slope and $b$ is the $y -$ intercept. The slope is how much $y$ changes for each unit change in $x$ . For any starting point $x$ if you move one step to the right to $x + 1$ , the new $y -$ value becomes $m (x + 1) + b = m x + m + b$ . Subtract $y = m x + b$ and all that's left is $m$ .

A step by $1$ in the $x -$ direction gives a change by $m$ in the $y -$ direction, which is the slope of the line.

If $x = 0$ , then $\times 0 + b = b$ so the $y -$ intercept is $b$ . Since two points define a line, then start at $b$ on the $y -$ axis, move to $x = 1$ and add $m$ (or subtract $m$ if $m$ is negative) to get a second point. Draw your line through the two points.

The line can also be defined as a function,

f (x) = m x + b .

Let's start by plotting some lines.

using-PlutoUI-Plots

We need a way to change the values of $m$ and $b$ . First, we'll make a slider for the slope $m$ and set the initial value to $m = 1$ .

m-slider

Next, we'll make a slider for $b$ and set it to $b = 0$ . Both can be varied between $- 5$ and $5$ .

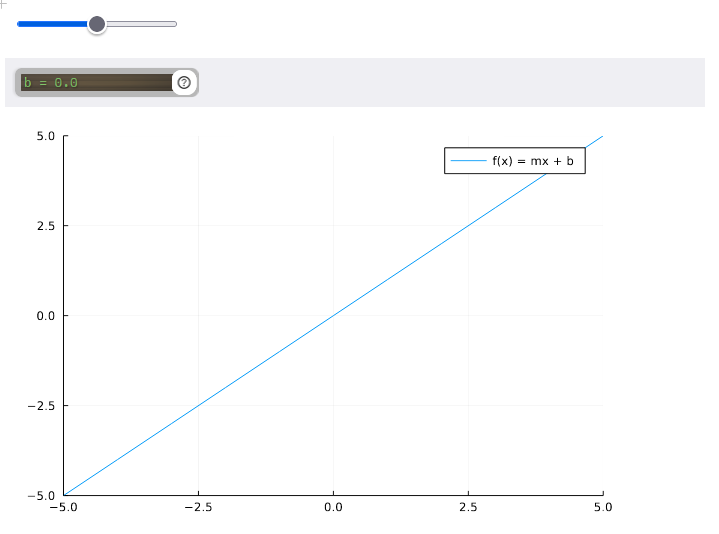
line-plot

Notice that the origin of the plot is in the center. Move the sliders for $m$ and $b$ to get a new plot. Interesting, but not chaos.

A Little Chaos¶

Chaos is doing nearly the same thing over and over and expecting wildly different results. Let's start with the linear equation above, with $m = 1$ and $b = - 1$ .

y = f (x) = x - 1.

Starting at $x = 1$ , the output of the function is $y = 0$ . Using this new value as the input, $f (0) = - 1$ . If you do this several times you get the uninteresting sequence

\{1,0,-1,-2,-3, \ldots \}.

Instead of calculating $x_1 = mx_0 + b$ and then $x_2 = mx_1 + b$ and so on, we can do this in a function iter_f with inputs $m,b,x_0,n$ where $x_0$ is the starting point, and $n$ is the number of iterations.

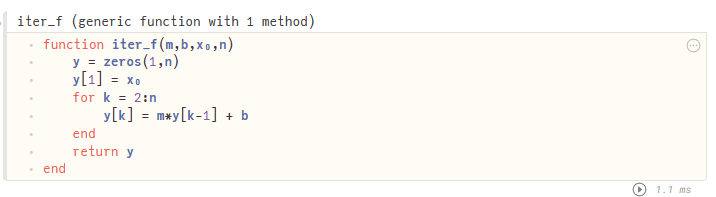
iter_f

We can try this function with the equation $y = x - 1$ starting at $x_0 = 0.4961$ and $x_1 = 0.4962$ for $n = 10$ iterations.

linear-results

Taking the difference between the outputs gives an uninteresting answer:

linear-differences

Now, let's change the equation slightly to $f (x) = 2 x - 1$ , and use the same starting points as before.

linear-2x

The difference between these sequences is:

differences-2x

Multiply the differences by $10000$ to make the changes more obvious:

differences-2x-10000

This is a little bit surprising, but notice that each number is twice the previous number. It looks like the sequence $\{ 2^0, 2^1, 2^2, \dots 2^9 \}$ and could be written as $2^{[0:9]}$ :

differences-pow2

Let's write out several iterations of $y = m x + b$ in terms of the starting point $x_0$ .

\begin{aligned} x_1 &= m x_0 + b \\ x_2 &= m x_1 + b = m (m x_0 + b) + b = m^2 x_0 + m b + b = m^2 x_0 + (m+1) b \\ x_3 &= m x_2 + b = m (m^2 x_0 + (m+1) b) + b = m^3 x_0 + (m^2 + m + 1) b \\ x_4 &= m x_3 + b = m (m^3 x_0 + (m^2 + m +1) b) + b = m^4 x_0 + (m^3 + m^2 + m + 1) b \\ \end{aligned}

The $n^{th}$ iterate in terms of $x_0$ is

x_n = m^n x_0 + (m^{n-1} + m^{n-2} + \cdots + 1) b.

What happens if we make a small change in $x_0$ ? If we change $x_0$ by a small amount, $\epsilon$ , then

\tilde{x}_n = m^n (x_0 + \epsilon) + (m^{n-1} + m^{n-2} + \cdots + 1) b

and the difference between the two results after $n$ iterations is (the term with $b$ is the same for both)

\tilde{x}_n - x_n = m^n (x_0 + \epsilon) - m^n x_0 = m^n \epsilon.

So long as $∣ m ∣ > 1$ then we can make $m^n \epsilon$ as big as we like by iterating enough times, no matter how small $\epsilon$ is. A small change to the initial value of $x_0$ produces as big a change as you like in the final value, $x_n$ .

There you have it. Chaos!

Moar Chaos¶

With a slightly more complicated equation, chaos becomes even more interesting. Instead of iterating a linear equation, let's use the logistic function (see The Growing Gap for an application of logistic functions)

F (x) = c x (1 - x) .

For $c = 4$ , this is an inverted parabola that has a maximum at $(0.5, 1.0)$ . If you draw the line $y = x$ it intersects the parabola at $(0, 0)$ and $(0.75, 0.75)$ . This line is useful for following the iterations or orbits of the function.

Start with a point on the $x -$ axis, say $x_0 = 0.2$ (point A). Find the value of $\times 0.2 \times (1 - 0.2) = 0.64$ . This point B is on the parabola above point A.

We want to iterate $F (x)$ by using the $y -$ coordinate of B as the next input. We could calculate $\times 0.64 \times (1 - 0.64) = 0.9216$ and we'll want to write a Julia function to do that, but it's also useful to see how the orbit evolves.

Draw a horizontal line until you get to the line $y = x$ at point C. Because C is on the $\degree$ line, then $x_C = y_C$ so the coordinates are $C = (0.64, 0.64)$ . The $x -$ coordinate of C is the $y -$ coordinate of B, so C becomes the next iterate. From C, draw a vertical line until you intersect the parabola at D which has coordinates $(0.64, 0.9216)$ .

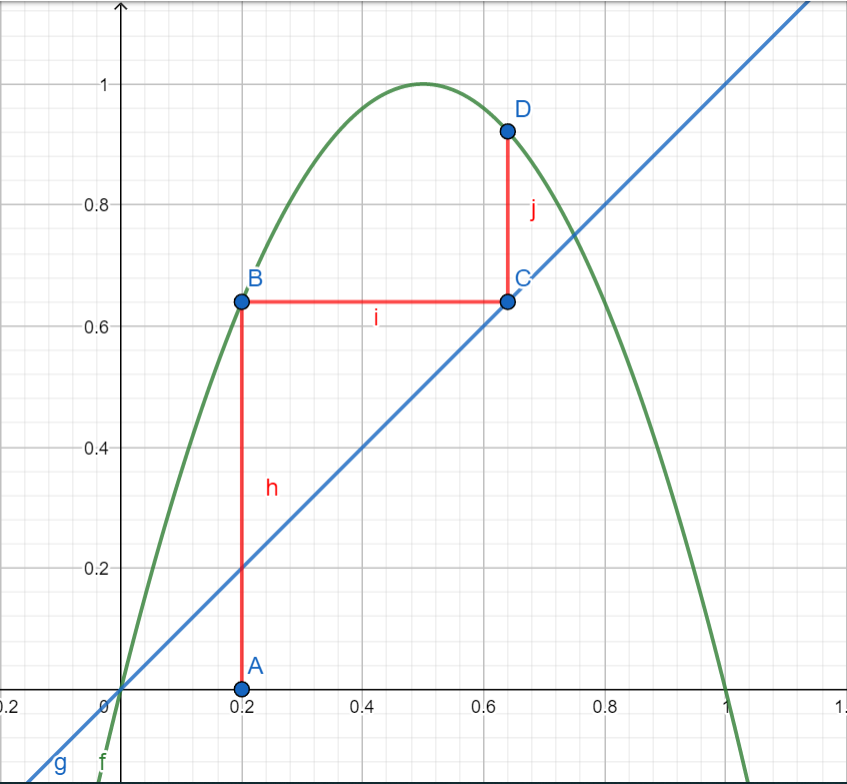
logistic-orbits

This process can be repeated as often as you like and will show the trajectory of the function $F (x)$ .

An Iterator for the Logistic Function¶

Like the iter_f function above, we can write a Julia function to iterate the logistic function. The inputs will be the starting point, $x_0$ , the constant $c$ , and the number of iterations $n$ with a default value of $n = 100$ .

This new function, iter_logistic will return the orbit, $y$ .

iter_logistic

Let's try an example with $x_0 = 0.2$

slider-x0

and $c = 4$ .

slider-c

y-logistic

Now we can plot the trajectory:

plot-y-logistic

Try adjusting the value for $c$ . When $c = 4$ the plot seems pretty chaotic. What happens if you change $x_0$ from $0.2$ to $0.19$ ? This should show that the trajectory is sensitive to the initial value of $x_0$ .

Next, try $c = 0.5$ and set $x_0 = 0.1$ . Is the plot chaotic? Is it sensitive to initial conditions?

Autocorrelation and Orbits¶

While the plot of the logistic function trajectory for $c = 4$ appears chaotic, you might be able to convince yourself that there are repeating patterns. The repetitions are far from identical, but if you imagine making a copy of the plot and shifting it over a bit, it might line up.

This is what autocorrelation does. The amount of the shift is controlled by a lag $\tau$ . For each $y [t]$ autocorrelation compares it to $\tau]$ . The output of the autocorrelation function is a number $r_k$ between $- 1$ and $1$ , where

r_k = \frac{\sum_{t = \tau + 1}^N (y[t] - \mu)(y[t - \tau] - \mu)}{\sum_{t=1}^N (y[t] - \mu)^2}

and $\mu$ is the average of all the $y$ 's. If $r_k = 1$ then $\tau]$ for every $t$ , $r_k = 0$ means there is no correlation, and $r_k = -1$ says that $\tau]$ .

A orbit is the plot of $y [k]$ on the $x -$ axis and $y[k+\tau]$ on the $y -$ axis.

Let's start by plotting the autocorrelation of the iterated logistic function for different values of $\tau$ .

Rather than scrolling back up to set $x_0$ and $c$ , let's just create two new variables and call them $x P$ and $c P$ .

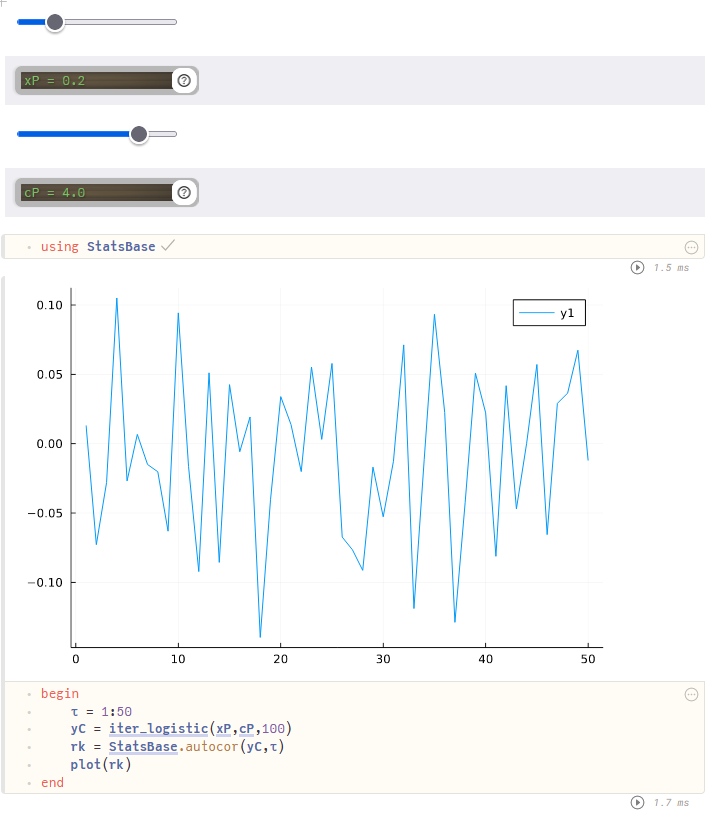
plot-autocorrelation

Choose the autocorrelation step $\tau$ :

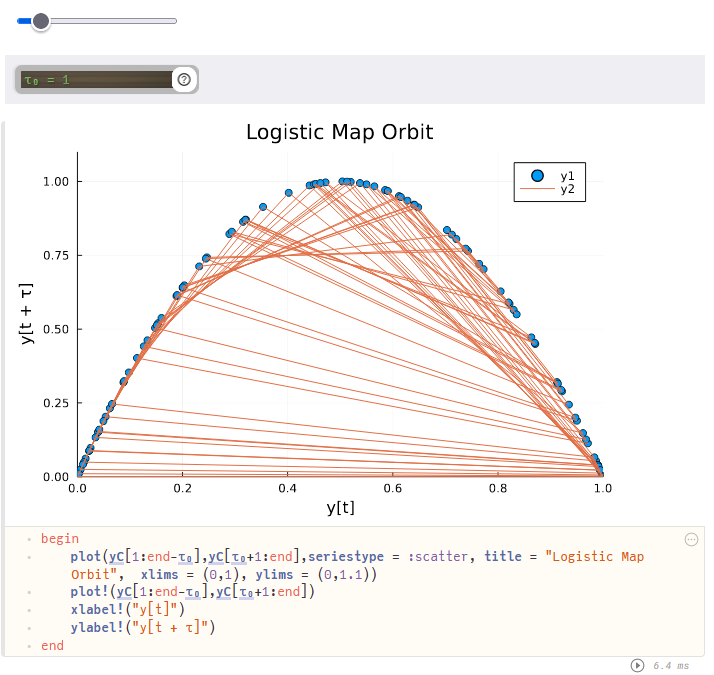
plot-phase-portrait

The autocorrelation plot seems about as chaotic as the logistic function, but when $\tau_0 = 1$ , the phase portrait is very smooth. In fact, the outline of the blue dots ( $y 1$ ) looks just like the logistic function!

This should be expected since $y_{n+1} = f(y_n)$ for every $n$ .

Why choose $\tau_0 = 1$ ? That choice of $\tau_0$ plots the orbit of the function. The orange lines (y2) show which point follows the current location. On the left side, the path seems to be mostly upwards towards a nearby point. On the right, points are sent back to the left half except those near $x = 1$ .

Try setting $\tau_0 = 0$ and you'll see that the orbit becomes the line $y = x$ , because there's perfect correlation between $y [t]$ and $\tau_0]$ . The plot doesn't provide any insight. Try some other values of $\tau_0$ to see what happens.

With Pluto, you can change the input values to a function to immediately see the effects.

Conclusion: Making Sense of the Unpredictable¶

Through our exploration with Pluto notebooks, we've seen how even simple mathematical rules can generate surprisingly complex behavior. We started with linear equations, where small changes in initial conditions lead to predictable differences in outcomes. Then, by making a slight modification to create the logistic function, we discovered how chaos emerges - where tiny differences in starting points can lead to wildly different results.

The key insights we've uncovered include:

Linear systems behave predictably, with differences growing in a steady, controlled manner
The logistic function, despite its simple form, can produce chaotic behavior when the parameter c is set appropriately
Chaos doesn't mean random - the phase portraits revealed beautiful structure within the apparent disorder
Interactive tools like Pluto notebooks allow us to experiment and visualize these complex dynamics directly

While chaos might seem to make prediction impossible, understanding chaos theory actually helps us better grasp the nature of complex systems - from weather patterns to population dynamics to heart rhythms. We now know that some systems have fundamental limits to predictability, not because of our ignorance or lack of precision, but because of their inherent sensitivity to initial conditions.

If you're interested in exploring further, try experimenting with:

Different values of the parameter $c$ in the logistic function
Various initial conditions to see how trajectories diverge
Other nonlinear functions to discover new types of chaotic behavior
Applying these concepts to real-world data sets

Remember: chaos isn't about things being completely unpredictable - it's about understanding the delicate balance between order and randomness that governs many of the complex systems in our world.

Image credits¶

Hero image from Introduction to Online Nonstochastic Control, Elad Hazan, Karan Singh, Research Gate, Figure 2.7: Lorenz attractor Nov 2022.

Code and Software¶

EasyChaos.jl - A Pluto notebook to do some simple experiments with chaos theory.

Julia - The Julia Project as a whole is about bringing usable, scalable technical computing to a greater audience: allowing scientists and researchers to use computation more rapidly and effectively; letting businesses do harder and more interesting analyses more easily and cheaply.
Pluto.jl - Pluto is an environment to work with the Julia programming language. Easy to use like Python, fast like C.